Rang einer Matrix

Größtmögliche Anzahl von linear unabhängigen Spalten einer Matrix. Rang 0 gilt nur für die Nullmatrix. Alle anderen Matrizen haben mindestens den Rang 1. Z.B. bei einer ( 4,4 )-Matrix ist der maximale Rang = 4.

Rang einer Matrix = rg( A ) ( A ist die Matrix ) = Spaltenrang

Die Maximalanzahl der linear unabhängigen Zeilen ( Zeilenrang ) ist identisch mit rg(A)

Folgerungen:

• A hat die Dimension ( m,n ), dann folgt daraus

• 

• <=> A = N ( Nullmatrix )

Beispiele:

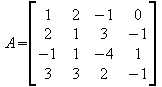
Zeile 1 + Zeile 2 = Zeile 4

Zeile 2 + Zeile 3 = Zeile 1

d.h. die Zeilen 1 und 4 sind als Linearkombinationen der Zeilen 2 und 3 darstellbar : rg(A) = 2

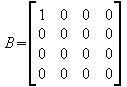
Die Spalten 2, 3 und 4 sind identisch, und ausserdem Nullspalten, und können deshalb gestrischen werden, da sie für den Rang der Matrix keine Rolle spielen : rg(B) = 1

Satz:

Ranggleichung : Für beliebige Matrizen B und C gilt :

für C = E gilt :

für B = E gilt :

Satz:

B quadratisch und regulär, gilt : und

Beweis:

daraus folgt :

Satz:

Jede quadratische Matrix A kann mit 2 regulären Matrizen B und C von links nach rechts so multipliziert werden, dass eine Diagonalmatrix D entsteht.

Daraus folgt :

daraus folgt :