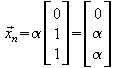Lösung
homogene Gleichungssysteme![]()
Es sei![]() A
= (m,n)-Matrix
A
= (m,n)-Matrix
Angenommen, die ersten r Gleichungen ( Zeilen von A ) sind linear unabhängig. Dann sind die restlichen ( m - r ) - Gleichungen linear abhängig von den ersten r Gleichungen, d.h. es gilt :
![]()
![]()
=> Lösung der ersten r Gleichungen, ist auch Lösung der restlichen Gleichungen
=> Es brauchen nur die ersten r Gleichungen betrachtet werden ( Vorraussetzung: sie sind lind linear abhängig ! )
Wir nehmen an:
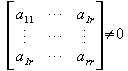
![]()
...
![]()
Gibt man beliebige Werte für die letzten n-r-Unbekannte vor, so erhält man ein quadratisches (r,r)-Gleichungssystem mit regulärer Koeffizientenmatrix => besitzt eine eindeutige Lösung !
Setzt man![]() .
.
Man
setzt![]()
![]()
![]()
=>![]() ist
Lösung
ist
Lösung
Man
setzt![]()
![]() analog
fortsetzen !
analog
fortsetzen !
=> Man bekommt
n-r-Lösungen !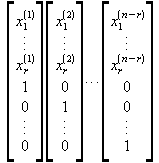
Satz:
![]() sind
linear unabhängig !
sind
linear unabhängig !
Beweis:
![]()
Ausmultiplizieren ergibt
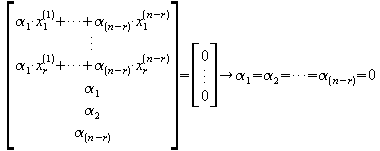 =>
linear unabhängig !
=>
linear unabhängig !
q.e.d.
=>![]() bilden
die Basis eines (n-r)-dimensionalen Vektorraumes.
bilden
die Basis eines (n-r)-dimensionalen Vektorraumes.
Dieser Vektorraum ist der Kern von A !
![]()
![]() =>
linear unabhängigen Spalten von A bilden eine Basis des Bildes
von A !
=>
linear unabhängigen Spalten von A bilden eine Basis des Bildes
von A !
Zeilen und Spalten sind nicht vertauschbar ! ! !
Beispiele :
rg(A) = n => Lösungsraum hat Dimension 0 => x = 0 ist einzige Lösung !
rg(A) = n-1 =>
Lösungen bilden einen eindimensionalen Vektorraum, d.h. es
gilt![]()
Satz :
Besitzt die
Koeffzientenmatrix A des homogenen linearen Gleichungssystems![]() mit
n Unbekannten den Rang 1, so gibt es n-r linear unabhängige
Lösungen.
mit
n Unbekannten den Rang 1, so gibt es n-r linear unabhängige
Lösungen.
Jede Lösung von![]() ist
eine Linearkombination der n-r linear unabhängigen Lösungen,
d.h. die allgemeine Lösung lautet:
ist
eine Linearkombination der n-r linear unabhängigen Lösungen,
d.h. die allgemeine Lösung lautet:![]() beliebig.
beliebig.
Beispiele :
![]()
![]()
![]()
n = 2 ; rg(A) = 1 ; dim(L) = n-rg(A) = 1
![]()
![]()
allgemeine Lösung
:![]() bzw.
bzw.![]()
![]()
![]()
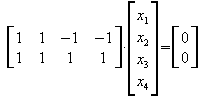
n = 4 ; rg(A) = 2 ; dim(L) = n-rg(A) = 4-2 = 2
![]()
![]()
![]()
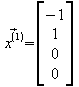
![]()
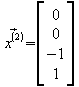
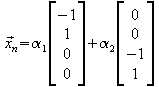
![]()
spezielle Lösungen :
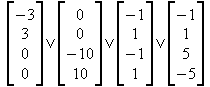
![]()
![]()
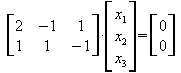
n = 3 ; rg(A) = 2 ; dim(L) = n-rg(A) = 1
![]()