Mathematik Grundkurs: Analysis

Gegeben sind eine Funktion und zwei Punkte, ermitteln Sie die Parameter.

1.AUFGABE:

k(x) = a(x+b)² P1 [2/3] P2 [-1/e]

Einsetzen von P1 und P2 in die Ausgangsfunktion:

3 = a(2+b)²

e = a(-1+b)²

a isolieren durch Division der Klammerausdrücke, dann gleichsetzen:

=

e(2+b)² = 3(-1+b)²

ausmultiplizieren:

4e+4eb+eb² = 3-6b+3b² |-3+6b-3b²

Gleichung Null setzen:

0 = (e-3)b² + (4e+6)b + 4e-3 |:(e-3)

0 = b² + +

quadratische Gleichung lösen:

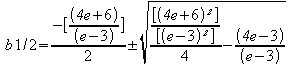
die Lösungen lauten:

b 1 = 60.35667

b 2 = -0.463028

Diese Ergebnisse werden in die Ausgangsgleichungen eingesetzt.

oder wahlweise in die andere Gleichung einsetzen:

Es ergeben sich also zwei Funktionsgleichungen:

k ( x ) = 0.0007715 ( x + 60.35667 )

k ( x ) = 1.269958 ( x – 0.463028 )

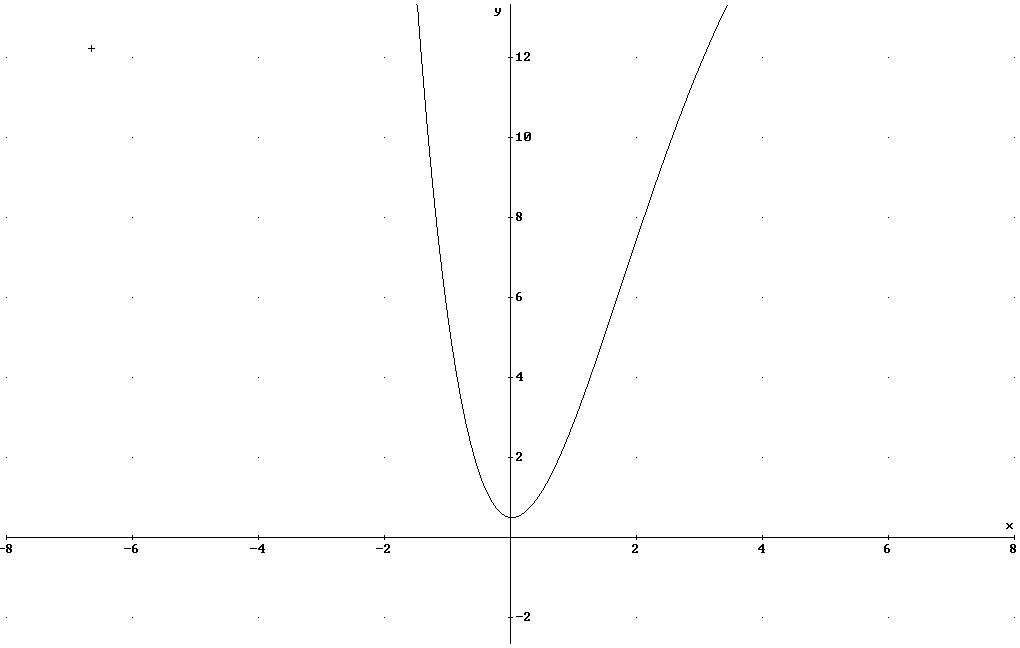
Graphische Darstellung:

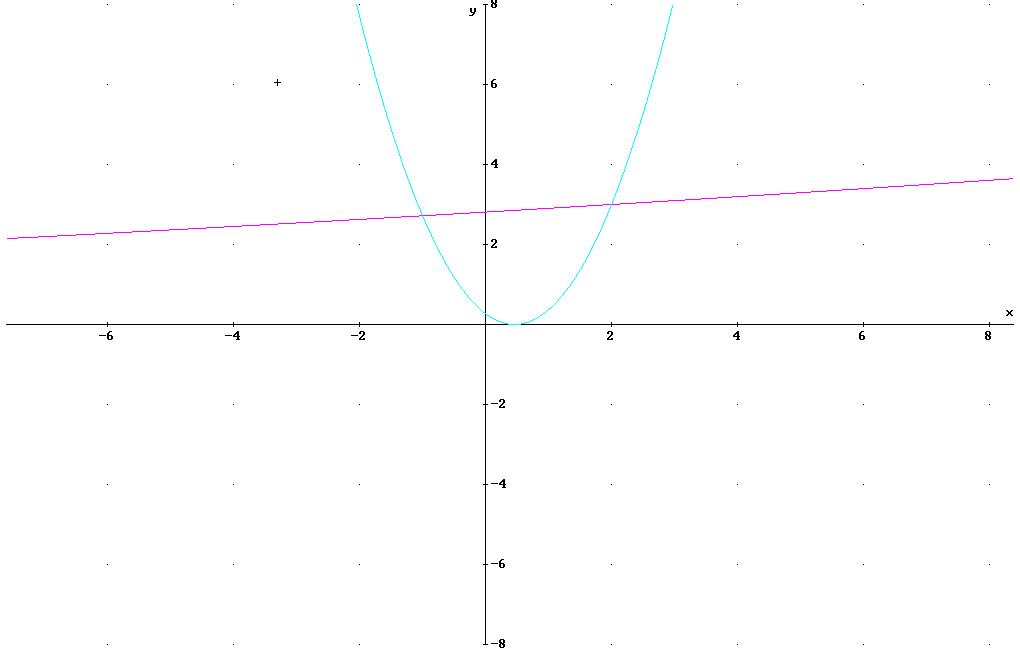
2.AUFGABE:

P1[1/] P2 [3/]

Einsetzen von P1 und P2 in die Ausgangsfunktion:

Gleichungen dividieren:

Kürzen auf:

| mal 8

| radizieren

| ln

n = 0.333333

Gleichung nach k umstellen:

Einsetzen von P 1\2 [x,y] und n:

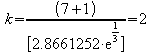
k = 2

Die Ausgangsfunktion mit den Parametern n und k lautet:

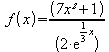
Graphische Darstellung: