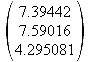Der Graph von fa ist Ga.ABITURPRÜFUNG-MATHEMATIK GRUNDKURS
1. Gegeben ist eine Funktionsschar fa durch ihre Funktionsgleichung
Der Graph von fa ist Ga.
1.1
Zeichnen Sie für den
Fall
den
Graph
in
ein kartesisches Koordinatensystem.
Berechnen Sie dazu die Koordinaten der Achsenschnittpunkte, der Lokalen Extrempunkte und des wendepunktes.
Y-ACHSE:
ASP [0/0]
X-ACHSE:
x1=0
nach
p-q-Formel lösen:
x2=6
x3=0=x1
PX 1 [0/0] PX 2 [6/0]
ABLEITUNGEN:
LOKALE
EXTREMA:
nach p-q-Formel lösen:
x1=6
x2=2
hinreichende Bedingung prüfen:
EP 1 [6/0]
EP 2 [2/8]
WENDEPUNKT:
|+6
|
mal
hinreichende Bedingung erfüllt
WP [4/4]
GRAPHISCHE DARSTELLUNG:
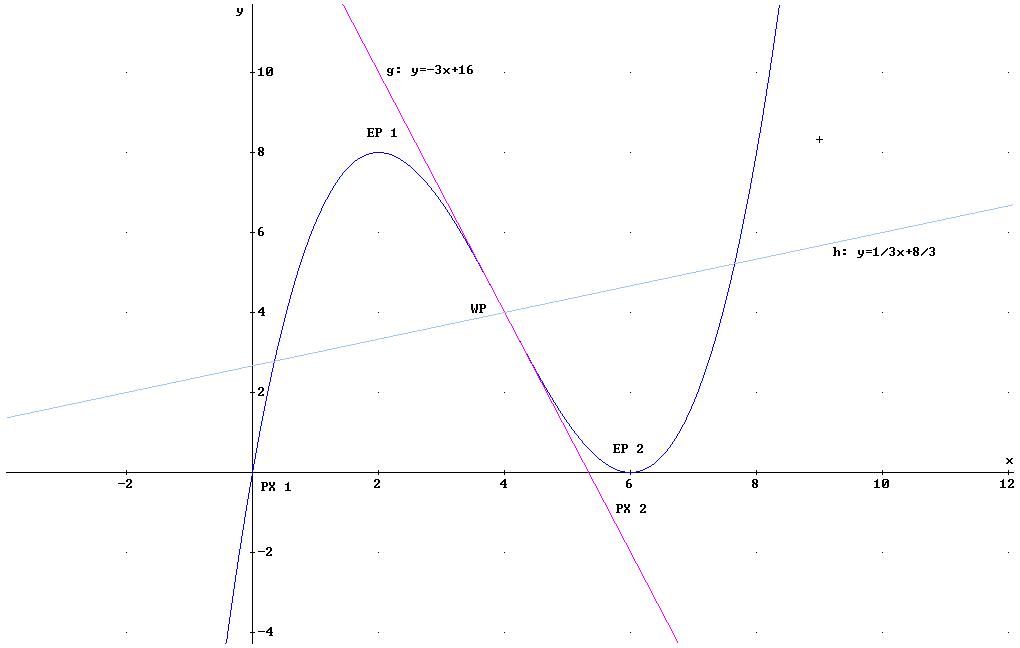
1.2
Die Gerade g sei eine Tangente an den Graph
im
Wendepunkt. Bestimmen Sie die Gleichung einer Geraden h, die
ebenfalls durch den Wendepunkt verläuft und zu g senkrecht ist.
TANGENTE
AM WENDEPUNKT WP [4/4]:
ORTHOGONALE
ZU g:
1.3
Gegeben sei eine Tangente k
mit der Gleichung y=x. Berechnen sie die Koordinaten aller
Schnittpunkte der Geraden k mit
.
Gleichungen
subtrahieren
x1=0
SP 1 [0/0]
nach
p-q-Formel lösen:
x2=4
SP 2 [4/4]
x3=8
SP 3 [8/8]
Für
wird
durch den Graph
und die Gerade k eine Fläche eingeschlossen. Berechnen Sie die
Maßzahl des Flächeninhaltes dieser Fläche.
=
=
=
=|-16|FE
1.4.
Durch den Punkt P [r/0] mit 0<r<3 und den Maximumpunkt
von
geht
eine Gerade. Diese teilt die von dem Graph
und
der x-Achse eingeschlossene Fläche in zwei Teile. Bestimmen sie
r so, dass die Fläche halbiert wird.
Zuerst errechnet man den gesamten Flächeninhalt und halbiert ihn dann:
=
=
=
=
27 FE :2 = 13.5 FE
Man integriert zunächst bis 2, damit man danach, je nach Bedarf, ein rechtwinkliges Dreieck addieren bzw. subtrahieren kann.
=
=
=
11 FE
Es fehlt also noch eine Fläche von 2.5 FE. Stellt man die Formel zur Flächenberechnung eines rechtwinkligen Dreiecks nach g um, so erhält man den Wert, welcher mit 2 addiert das gesuchte r ergibt.
GRAPHISCHE DARSTELLUNG:
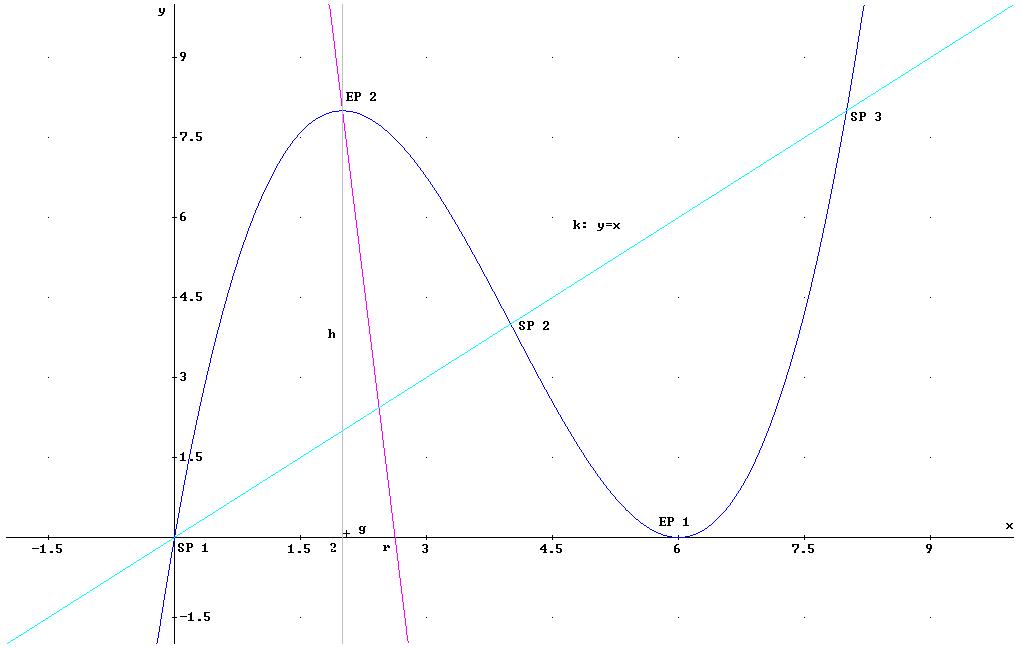
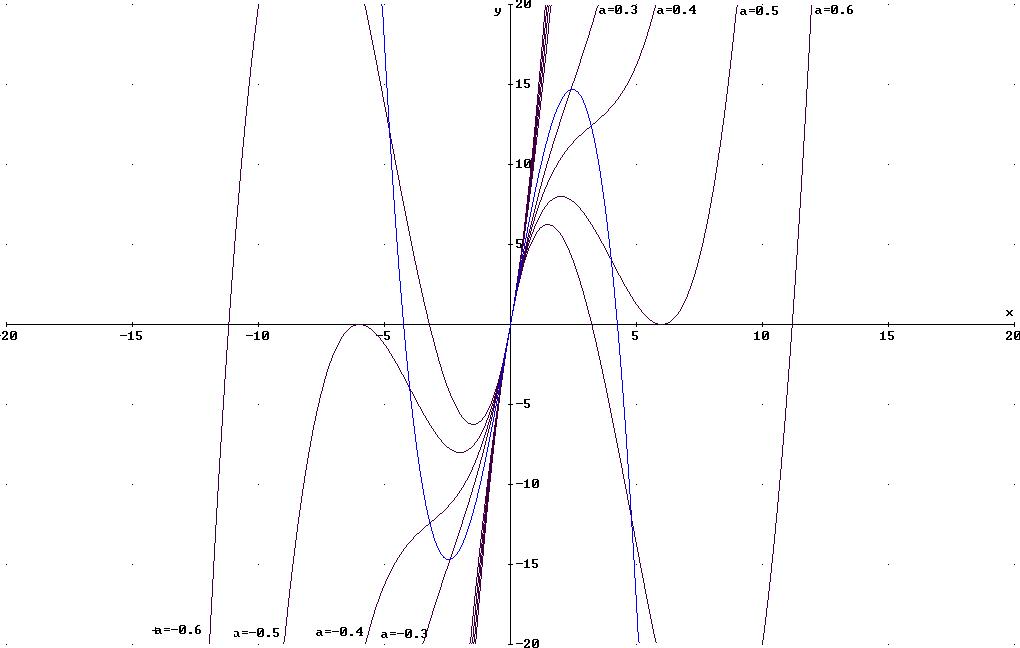
1.5 Berechnen
Sie die Gleichung jener Funktion auf deren Graph alle Wendepunkte
von
liegen.
Zuerst errechnet man den Wendepunkt allgemein für a:
hinreichende
Bedingung erfüllt
Normalform
herstellen:
Der Wendepunkt für beliebige a liegt bei WPa [8a/-256a³+72a]
Wir stellen nun x=8a nach a um und setzen dieses ein:
GRAPHISCHE
DARSTELLUNG FÜR DEN BEREICH
2. Eine Funktionsschar fb, ist durch folgende Gleichung gegeben:
Ihr Graph ist
.
2.1 Geben Sie in Abhängigkeit von b die Koordinaten der Achsenschnittpunkte, der lokalen Extrempunkte und der Wendepunkte an.
Y-Achse: x=0
y=0
ASP [0/0]
X-ACHSE:
y=0
x1=0
PX 1 [0/0]
die
e-Funktion wird nie Null, keine weiteren Nullstellen
ABLEITUNGEN:
EXTREMA:
die
e-Funktion wird nie Null
x=1
hinreichende Bedingung
prüfen:
WENDEPUNKT:
die
e-Funktion wird nie Null
x=2
hinreichende Bedingung
prüfen:
erfüllt
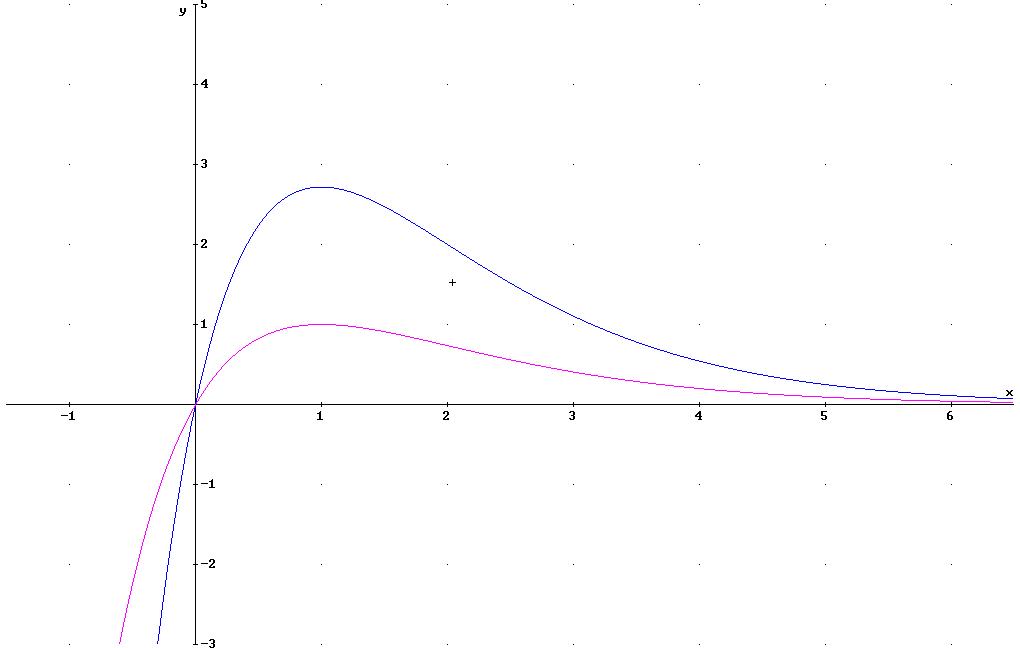
2.2 Zeichnen
Sie die Graphen
und
in
ein kartesisches Koordinatensystem.
2.3 Bestimmen
Sie den Parameter b für den Fall, dass der Graph der Funktion fb
den Punkt P [3/5] durchläuft. Welchen Anstieg hat der
entsprechende Graph im Punkt P?
|:3 
|ln 
|+3 
2.4 Zeigen
Sie, dass die Funktion Fb mit
eine
Stammfunktion von fb ist.
Die
Gerade mit der Gleichung x=b (b>0) schließt mit dem
Graphen
und
der x-Achse eine Fläche ein. Berechnen Sie die Maßzahl
des Flächeninhaltes in Abhängigkeit von b.
=
=
=
=
3. In ein räumliches kartesisches Koordinatensystem sind die Geraden g und h mit den Gleichungen gegeben.
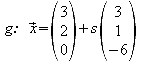
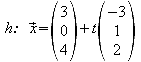
3.1 Ermitteln Sie den Schnittpunkt dieser Geraden.
|
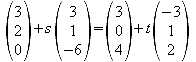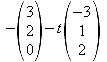
x 0=3s+3t x 6=3s+3t
y
-2=s-t
6y+z=z' y
2=s-t
z 4=-6s-2t z' -8=-8t
1=t -2=s-1 |+1
-1=s
Probe:
bestätigt
bestätigt
bestätigt
Schnittpunkt:
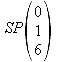
3.2 Bestimmen Sie die Parametergleichungung und die Koordinatengleichung für die Ebene E, die beide Geraden enthält.
Die Parametergleichung lautet:
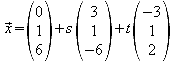
X=3s-3t
x+3y=3+6s
y=1+s+t 
4(x+3y)+3(-2y+z)=24
|:24
z=6-6s+2t
-2y+z=4-8s
Doppelbruchregeln
anwenden
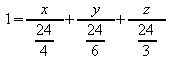
Die
Koordinatenform lautet:
3.3 Berechnen Sie den Schnittwinkel der Ebene E mit der x-y-Ebene.
4x+6y+3z-24=0 
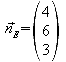Normalenvektor der x-y-Ebene:
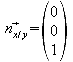
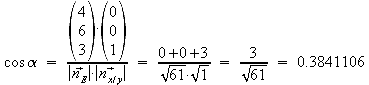
3.4 Geben Sie die Koordinaten derjenigen Punkte A, B und C an, die die Ebene E mit den Achsen des Koordinatensystems gemeinsam hat.
X-Achse:
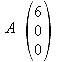y-Achse:
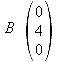z-Achse:
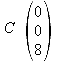
3.5 Berechnen Sie den Flächeninhalt des Dreiecks ABC.
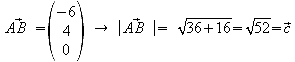
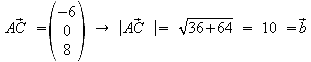
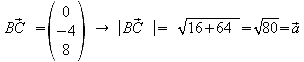
heronische Formel:
mit
=
3.6 Gegeben ist weiterhin ein Punkt P(-1/-5/-2). Berechnen Sie das Volumen der Pyramide, die durch das Dreieck ABC als Grundfläche und den Punkt P als Spitze bestimmt ist.
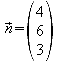(siehe
3.3)
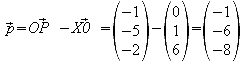
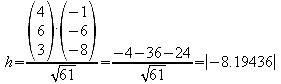
3.7 Bestimmen Sie den Spiegelpunkt P* von P bezüglich der Ebene E.
=
=
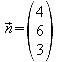
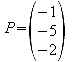
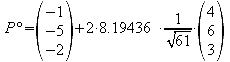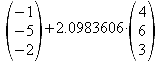