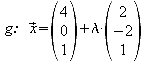
MUSTERKLAUSUR ANALYTISCHE GEOMETRIE
Gegeben sind in einem kartesischen Koordinatensystem die Punkte A(7;3;1) und B(1;-3;1) sowie die Gerade
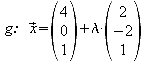
1. Die Punkte A und B liegen spiegelbildlich bezüglich einer Ebene E.
1.1 Bestimmen Sie eine Gleichung der Ebene in Normalenform.
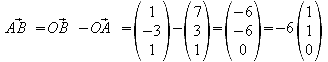
Der
erhaltene Vektor entspricht dem Normalenvektor der Ebene E, weil er
senkrecht zu ihr ist. Der Einheitsnormalenvektor lautet also
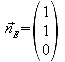
M
als Mittelpunkt von![]() liegt
direkt auf der Ebene.
liegt
direkt auf der Ebene.
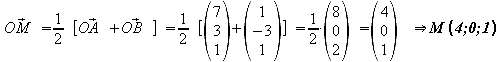
Einsetzen
von
![]() und
M in die Gleichung der hessischen Normalform:
und
M in die Gleichung der hessischen Normalform:
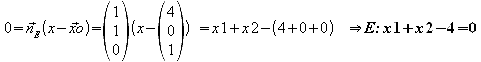
1.2 Welche besondere Lage hat die Ebene E im Koordinatensystem ?
Die Ebene E ist parallel zur z-Achse.
1.3. Weisen Sie nach, dass die Gerade g in der Ebene E liegt.
Der Festpunkt xo der Geraden g ist mit dem Festpunkt M der Ebene E identisch (siehe 1.1). Wenn der Einheitsnormalenvektor der Ebene E auch senkrecht zum Richtungsvektor der Geraden g ist, dann liegt die Gerade g in der Ebene E.
Nach
dem Skalarprodukt gilt:![]()
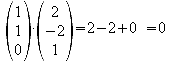 Bedingung
erfüllt.
Bedingung
erfüllt.
2. Vom Koordinatenursprung O wird das Lot auf die Gerade g gefällt.
2.1 Berechnen Sie die Koordinaten des Lotfußpunktes L.
L
liegt auf der Geraden g: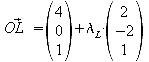
![]() muss
senkrecht auf der Geraden g stehen, deshalb gilt nach dem
Skalarprodukt:
muss
senkrecht auf der Geraden g stehen, deshalb gilt nach dem
Skalarprodukt:![]()
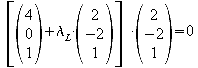
![]()
![]()
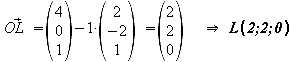
2.2 Auf der Geraden g sind nun zwei Punkte P1 und P2 so zu bestimmen, dass die rechtwinkligen Dreiecke OLP1 und OLP2 jeweils einen Flächeninhalt
von![]() besitzen.Berechnen
sie die Koordinaten der Punkte P1 und P2.
besitzen.Berechnen
sie die Koordinaten der Punkte P1 und P2.
P1 und P2 liegen auf g:
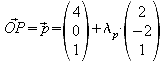
![]()
![]()
![]()
![]()
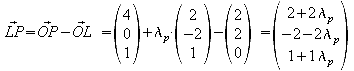
![]()
![]()
![]()
![]()
![]()
In
![]() :
:
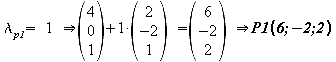
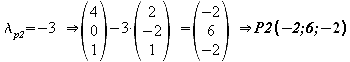
3. Durch den Koordinatenursprung O und den Punkt A ist die Gerade h festgelegt.
3.1 Geben Sie eine Gleichung der Geraden h an.
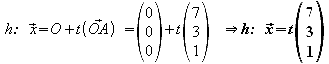
3.2 Berechnen Sie die Koordinaten des Schnittpunktes S der Geraden h mit der Ebene E.
![]()
![]()
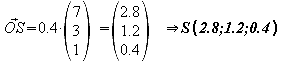
3.3 Untersuchen Sie, ob die Geraden g und h eine Ebene F aufspannen, und stellen Sie gegebenenfalls je eine Gleichung der Ebene F in Parameter- und Normalenform auf.
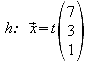
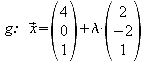
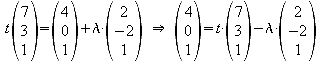
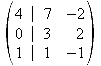
2.Zeile + 2 mal 3.Zeile = neue 3.Zeile
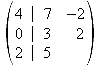
1.Zeile + 2.Zeile = neue zweite Zeile
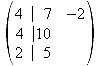
2.Zeile + 3.Zeile mal -2 = neue 3.Zeile
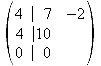
![]()
![]()
![]() Probe
bestätigt
Probe
bestätigt
![]() Probe
bestätigt
Probe
bestätigt
Der Schnittpunkt liegt bei SP [4/0/1]. Somit können die Gerade g und h eine Ebene F aufspannen.
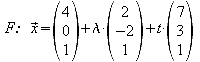
Um die Normalenform aufzustellen, benötigt man den Einheitsnormalenvektor dieser Ebene. Dazu wird das Vektorprodukt der beiden Richtungsvektoren
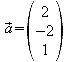 und
und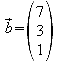 ermittelt.
ermittelt.
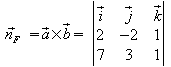 =
=![]() =
=
![]() =
=
![]() =
=
![]() =
=
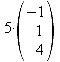
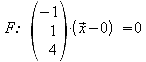
![]()