Klausur Mathematik Grundkurs
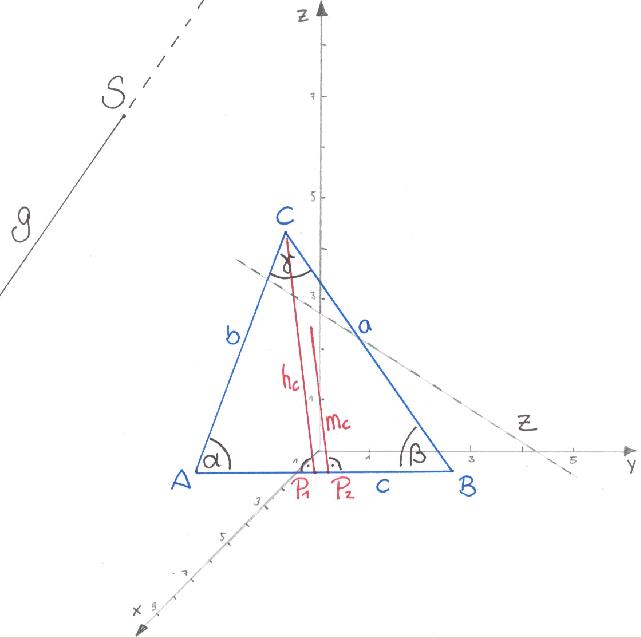
1. Gegeben ist ein Dreieck ABC durch seine Eckpunkte A[4/-1/1], B[1/3/0],
C[-1/-1/4]
a) Fertigen Sie eine perspektivische Zeichnung an.

b) Berechnen Sie näherungsweise die Seitenlängen, die Winkel und den Flächeninhalt dieses Dreieckes!
![]()
![]()
![]()
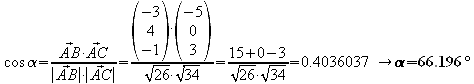
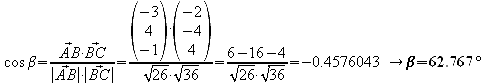
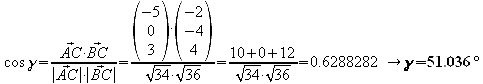
![]()
![]()
![]()
c) Das Dreieck ABC liegt in der Ebene E. Berechnen Sie deren Einheitsnormalenvektor.
Parametergleichung:
![]()

Normalenvektor:
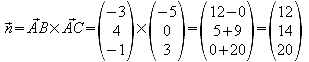
Normieren: 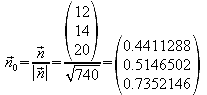
d) Wo durchstoßen die Achsen des Koordinatensystems diese Ebene?
kartesische
Form:
![]()
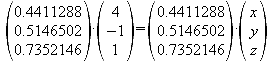
![]()
Achsenabschnittsform: ![]()
![]()
Koordinaten:
x-Achse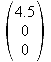 y-Achse
y-Achse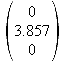 z-Achse
z-Achse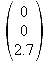
e) Welchen Abstand hat E vom Koordinatenursprung?
![]()
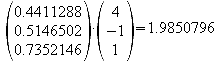
f) E durchdringt die y-z-Ebene in der Schnittgeraden h. Ermitteln Sie die Gleichung von h in der expliziten Form.
y-z-Ebene: x=0
![]()
![]()
![]()
g) In welchem Winkel steht E zur x-y-Ebene?
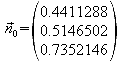
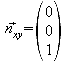
![]()
h) Wie liegt folgende Gerade g zum gegebenen Dreieck (Lagebeziehung, Winkel)?
g:
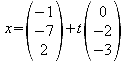
Gleichsetzen von Ebene E und Gerade g:
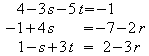
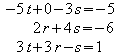 3
mal 1.Zeile + 5 mal 3.Zeile = neue 1.Zeile
3
mal 1.Zeile + 5 mal 3.Zeile = neue 1.Zeile
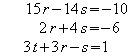 2
mal 1.Zeile - 15 mal 2.Zeile = neue 1.Zeile
2
mal 1.Zeile - 15 mal 2.Zeile = neue 1.Zeile
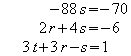
![]()
![]()
![]()
Schneidet
die Ebene im Punkt
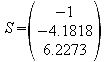
Der Schnittpunkt liegt außerhalb des gegebenen Dreiecks ABC.
Winkel der Gerade h zum Dreieck ABC:
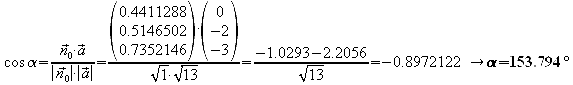
Dies ist der Winkel zwischen der Gerade und dem Normalenvektor der Ebene. Damit man den Winkel zwischen Gerade und Ebene erhält, muss man noch 90° abziehen.
![]()
i) Ermitteln Sie die Gleichungen der Höhe und der Mittelsenkrechten auf Seite AB. Welche Koordinaten haben die Fußpunkte P1 und P2 dieser Linien auf der Strecke AB?
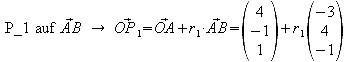
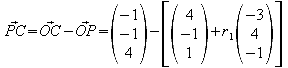
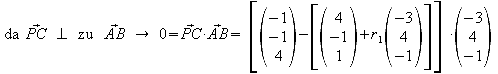
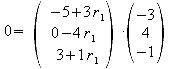
![]()
![]()
![]()
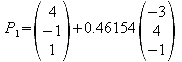
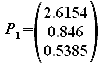
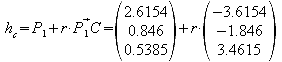
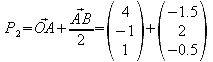
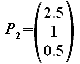
Da die Mittelsenkrechte ebenfalls orthogonal zu AB ist, kann man den gleichen Richtungsvektor wie bei der Höhe verwenden.
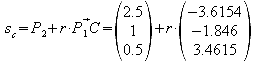
2. Gegeben ist ein Oktaeder durch seine Eckpunkte:
A[4/4/0]
B[4/8/0] C[8/8/0] D[8/4/0] E[6/6/![]() ]
F[6/6/
]
F[6/6/![]() ]
]
a) Zeichnen Sie den Körper perspektivisch in ein Koordinatensystem.
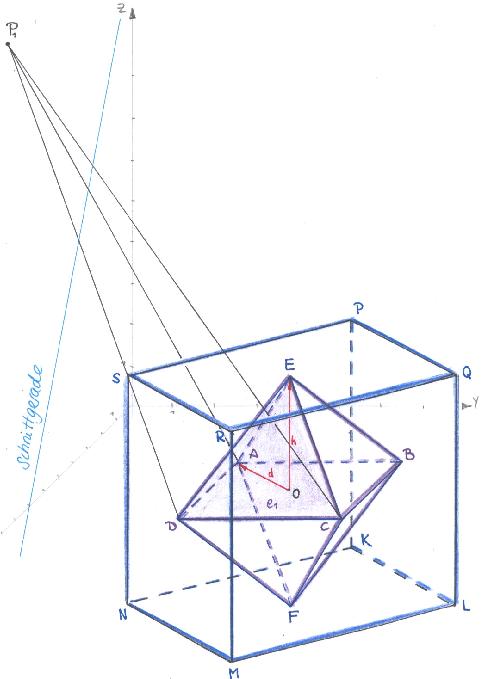
b) Stellen Sie die Parametergleichungen der drei Geraden auf, die seine Kanten DE, CD, CE enthalten.
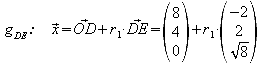
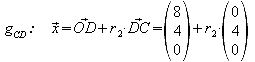
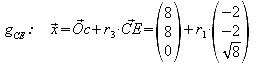
c) Berechnen Sie die Länge der Strecke CE.
![]()
d) Eine Ebene e1 enthalte den Punkt C und die Strecke DE. Bestimmen Sie zu dieser Ebene zuerst eine Parametergleichung, daraus dann die Achsenabschnittsgleichung und den Einheitsnormalenvektor.
Parametergleichung: ![]()
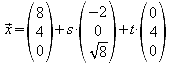
Einheitsnormalenvektor: ![]()
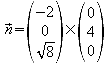 =
=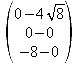 =
=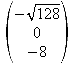
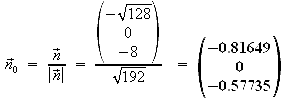
Achsenabschnittsform: ![]()
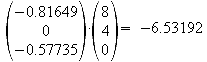
![]()
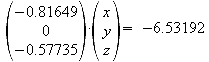
![]()
![]()
![]()
e) Bestimmen sie die Gleichung der Schnittgeraden in ihrer expliziten Form!
![]()
![]()
![]()
f) Ermitteln Sie den Abstand des Punktes P1 [3/-2/10] von e1.
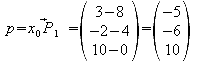
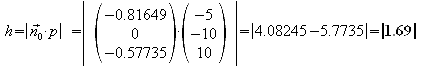
g) Bestimmen Sie auch die Abstände der Punkte A, C und D von P1 und stellen Sie fest, welche Winkel die Strecken P1 A, P1 C und P1 D jeweils zueinander haben.
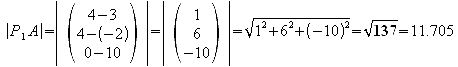
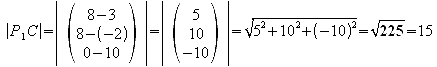
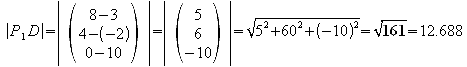
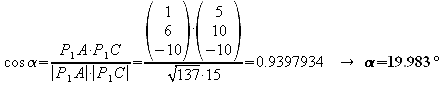
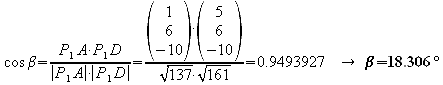
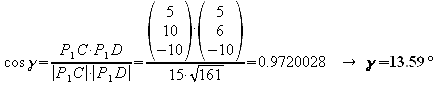
h) Bestimmen Sie die Eckpunkte KLMN PQRS des Würfels, der das Oktaeder derart enthält, dass die Eckpunkte des Oktaeders die Flächenmitten des Würfels berühren.
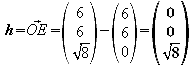
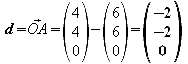
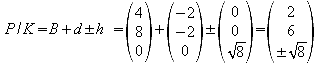
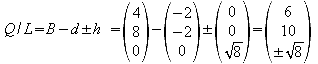
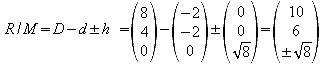
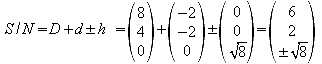
i) Wieviel Prozent des Würfelvolumens nimmt der einbeschriebene Körper ein?
Würfelvolumen: ![]()
Oktaedervolumen: ![]()
Relation: ![]()
![]()
3. Gegeben ist eine Funktion z durch die Gleichung
![]()
a) Stellen sie deren Bild in einem kartesischen Koordinatensystem dar.
Ableitungen: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Achsenschnittpunkte:
y-Achse:
![]()
![]()
![]() PY
[0/0]
PY
[0/0]
x-Achse:
![]()
![]()
![]()
![]()
![]() PX
[0/0]
PX
[0/0]
Extrema:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
EP1 [4/2.165] EP2 [0/0]
Wendepunkte:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
WP1 [6.828/1.534] WP2 [1.171/0.764]
Verhalten im Unendlichen:
![]()
![]()
Graphische Darstellung:
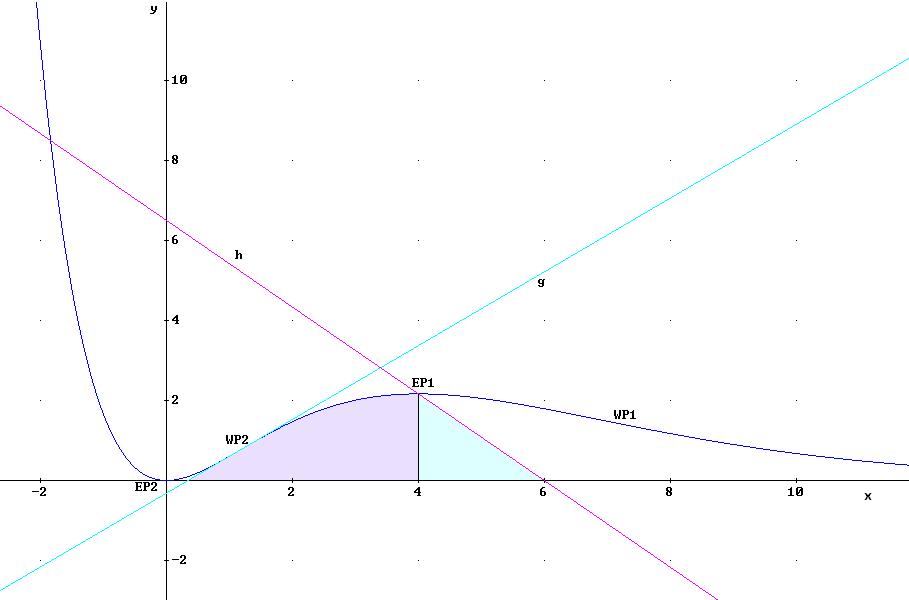
b) Welchen Anstieg hat die Tangente g am Wendepunkt zwischen den beiden lokalen Extrema?
WP2 [1.171/0.764]
![]()
![]()
c) Geben sie die Gleichung der Geraden h an, die zur Wendetangente g senkrecht steht und zugleich das lokale Maximum des Graphen von z schneidet.
![]()
![]()
![]()
d) Berechnen Sie den Inhalt des Flächenstückes, welches von z, h und der
x-Achse umgrenzt wird.
Man berechnet beide Flächeninhalte separat. Beginnend mit der Fläche A1 unter der Kurve z(x) mit den Integrationsgrenzen von 0 bis 4.
Um
die Stammfunktion bilden zu können, muss![]() zuerst
partiell integriert werden.
zuerst
partiell integriert werden.
Partielle
Integration:
![]()
![]()
![]()
2.
Teil: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Die zweite Fläche wird von der Gerade h eingeschlossen, ihr Schnittpunkkt mit der x-Achse entspricht der zweiten Integrationsgrenze.
![]()
![]()
![]()
![]()
![]()
![]()
![]()