AUFGABE 1:

Gegeben ist eine Funktion f durch ihre Gleichung

1.1 Berechnen Sie f(1) und f(8).

1.2 Berechnen sie die Nullstelle und den lokalen Extrempunkt von f und zeichnen Sie den Graph!

Nullstelle:

Ableitungen:

Extrempunkt:

EP [ e / e ]

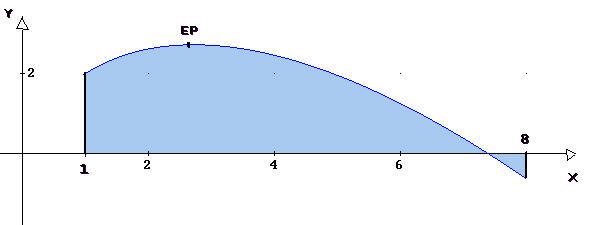
Graph:

1.3 Weisen Sie nach, dass die Stammfunktion von f ist.

1.4 Berechnen Sie den Inhalt der Fläche, die im gegebenen Intervall vom Bild der Funktion f und der x-Achse eingeschlossen wird.

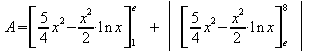
1.5 Gegeben sind die Funktionen g durch

P1 [1/a] ist ein Punkt der Graphen dieser Funktionen.

Ermitteln Sie den Parameter a für den Fall, dass die Tangente in P1

an den Graphen der entsprechenden Funktion den Anstieg 1 hat !

PROBE:

Gleichung der Tangente in P1

Probe bestätigt!

Für den Parameter a=2 hat die Tangente in P1 den Anstieg 1.

Aufgabe 2:

Drei Punkte P[1/1/1], Q[3/2/3], S[0/3/2] im kartesischen Koordinatensystem sind gegeben.

2.1 Stellen Sie eine Gleichung für die Gerade g auf, die durch die Punkte P und S verläuft und ermitteln Sie die Spurpunkte von g in den Koordinatenebenen.

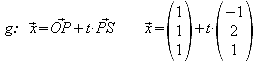
Spurpunkt in der y-z-Ebene:

P₁ [0/3/2]

Spurpunkt in der x-z-Ebene:

P₂ [1.5/0/0.5]

Spurpunkt in der x-y-Ebene:

P₃ [2/-1/0]

2.2 Eine Ebene E enthält die Gerade g und den Punkt Q. Geben Sie eine Gleichung für E in Parameterform sowie in Koordinatenform und Achsenabschnittsform an.

Parameterform:

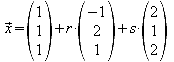
Normalenform: Normalenvektor: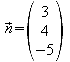

Achsenabschnittsform: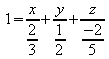

2.3 In welchem Winkel durchstößt die z-Achse die Ebene E ?

Normalenvektor von E: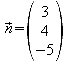 z-Achse: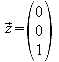

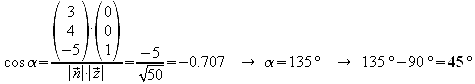
Da der Normalenvektor orthogonal zu E ist, müssen diese 90° noch subtrahiert werden.

2.4 Errechnen Sie die Koordinaten des Punktes R, der mit den gegebenen Punkten zusammen ein Parallelogramm bildet.

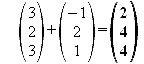R [2/4/4]

2.5 Durch die Spiegelung des Parallelogramms an der x-z-Ebene und die Verbindung der einander zugehörigen Punkte entsteht ein Körper. Zeichnen sie diesen und berechnen Sie seine Oberfläche.

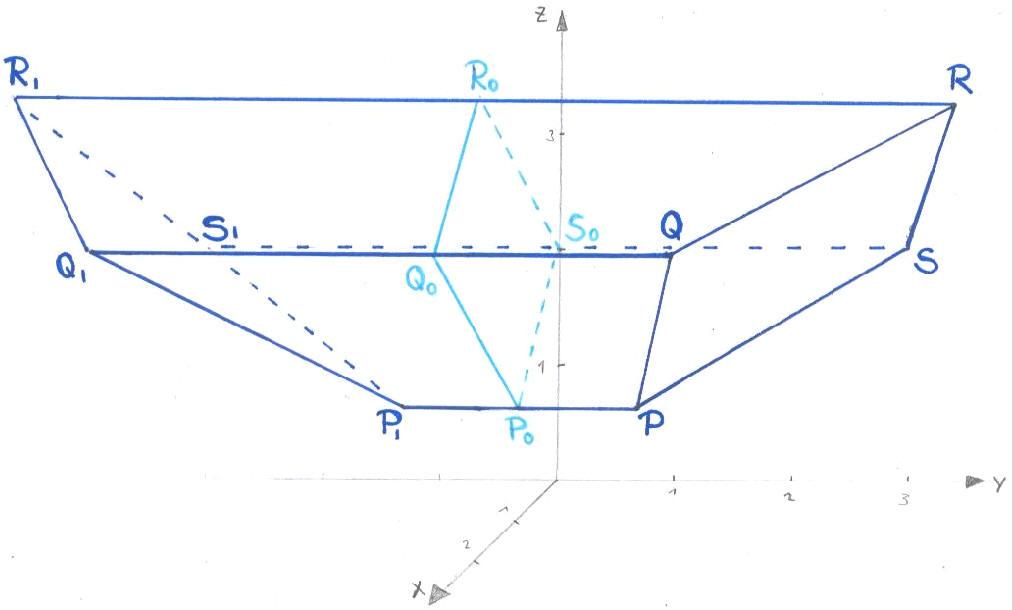
Berechnung der Oberfläche:

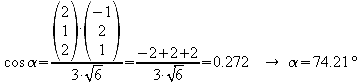
3.Aufgabe:

Gegeben ist eine Funktion f durch die Gleichung

3.1 Bestimmen Sie die dritte Ableitung von f.

3.2 Ermitteln Sie die Polstellen für f und berechnen Sie alle Achsenabschnittspunkte und lokalen Extrempunkte des Graphen.

Führen Sie den Nachweis, dass f bei x=4 eine Wendestelle hat.

Polstellen:

Für die ermittelten x wird der Zähler nicht Null.

x-Achse:

Für das ermittelte x wird der Nenner nicht Null.

y-Achse:

Extrempunkte:

Für die ermittelten x wird der Zähler nicht Null (siehe Polstellen).

Wendestelle:

Für x=4 wird der Nenner nicht Null.

3.3 Zeichnen Sie das Bild im Intervall in ein kartesisches Koordinatensystem.

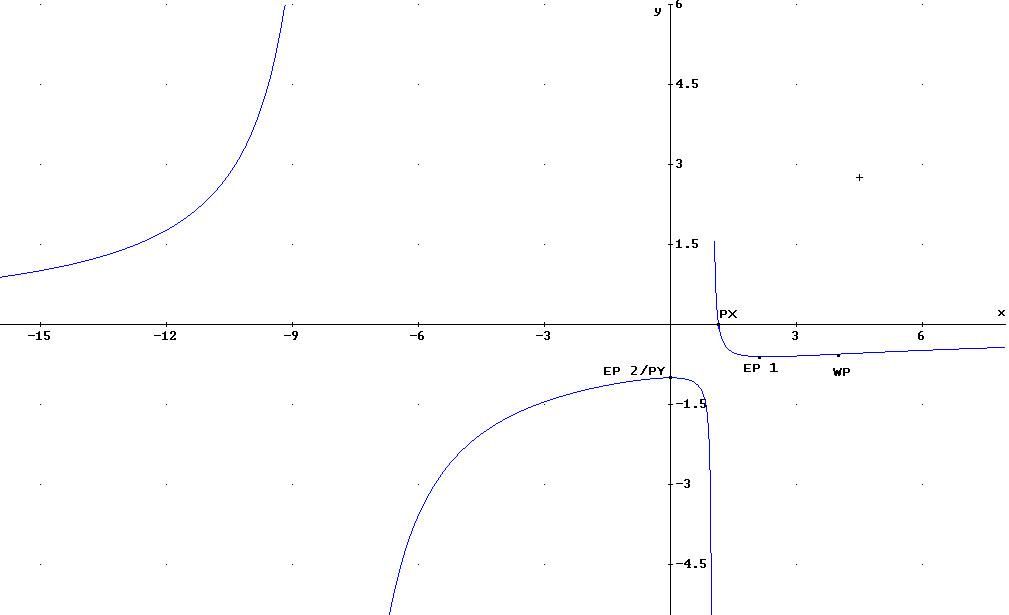
3.4 Ermitteln Sie die Gleichung der Tangenten h an Punkt A [3/f(3)]

3.5 Errechnen Sie den Flächeninhalt des Dreieckes, welches h mit den Koordinatenachsen bildet.
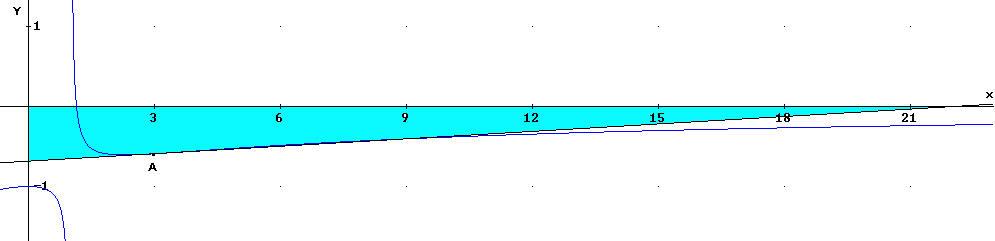