Gegeben ist eine Funktion, welche durch die Punkte A und B verläuft. Bestimmen Sie zuerst die Parameter a und b und führen Sie anschließend eine vollständige Kurvendiskussion durch.

Einsetzen der Punkte A und B in die Ausgangsgleichung:

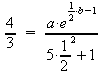
Zuerst vereinfachen: Gleichungen dividieren:

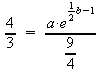
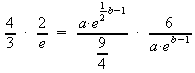
Kürzen und zusammenfassen:

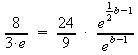
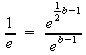NR:

Parameter b in eine der beiden Gleichungen einsetzen:

Die Funktion mit eingesetzten Parametern lautet also:

Definitionsbereich:

Ableitungen:

=

=

Achsenschnittpunkte:

y-Achse: x=0

x-Achse: y=0 wird nie Null keine Nullstellen

lokale Extrema:

hinreichende Bedingung:

EP1 [0.723607/1.29679]

EP2 [0.276393/1.38804]

Wendestellen:

Probieren:

x1 ca. -0.1

x2 ca. 0.45

Newton'sches Näherungsverfahren:

x1=-0.0986916 x2=0.4423159

(Es könnten noch weitere wendestellen existieren, diese könnten

durch Polynomdivision ermittelt werden. An dieser Stelle soll

auf diesen Aufwand verzichtet werden.)

hinreichende Bedingung:

WP [-0.0986916/0.8638792] WP[0.4423159/1.3512746]

Symmetrie: keine Symmetrie

Monotonieverhalten: x1=0.27 x2=0.44 x3=0.73

Verhalten im Unendlichen:

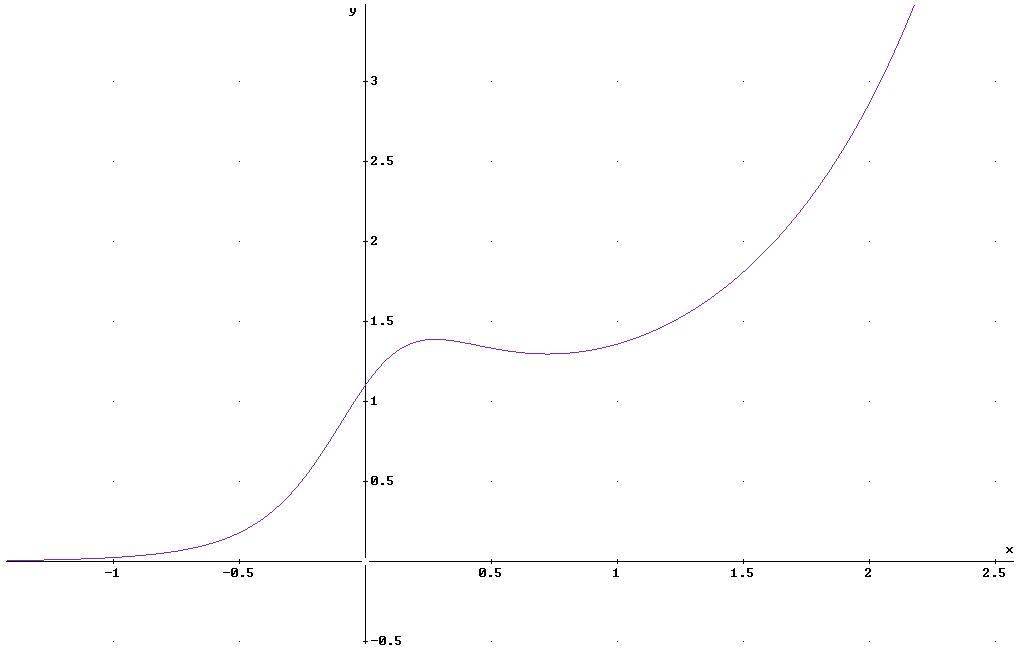
Graphik:

Führen Sie eine vollständige Kurvendiskussion an folgender Funktion durch:

Polstellen:

Achsenschnittpunkte:

y-Achse: PY[-1.1111/0]

x-Achse:

keine Nullstellen

Ableitungen:

=

=

lokale Extrema:

EP = PY[-1.1111/0]

hinreichende Bedingung:

Wendestellen:

keine Wendestellen

Verhalten an den Polgeraden:

Verhalten im Unendlichen:

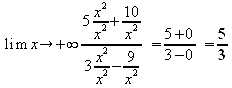
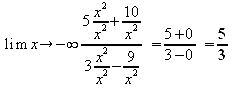
symmetrieverhalten:

symmetrisch zur y-Achse

Monotonieverhalten: x1= -1.7 x2= -1 x3= 1 x4= 1.75

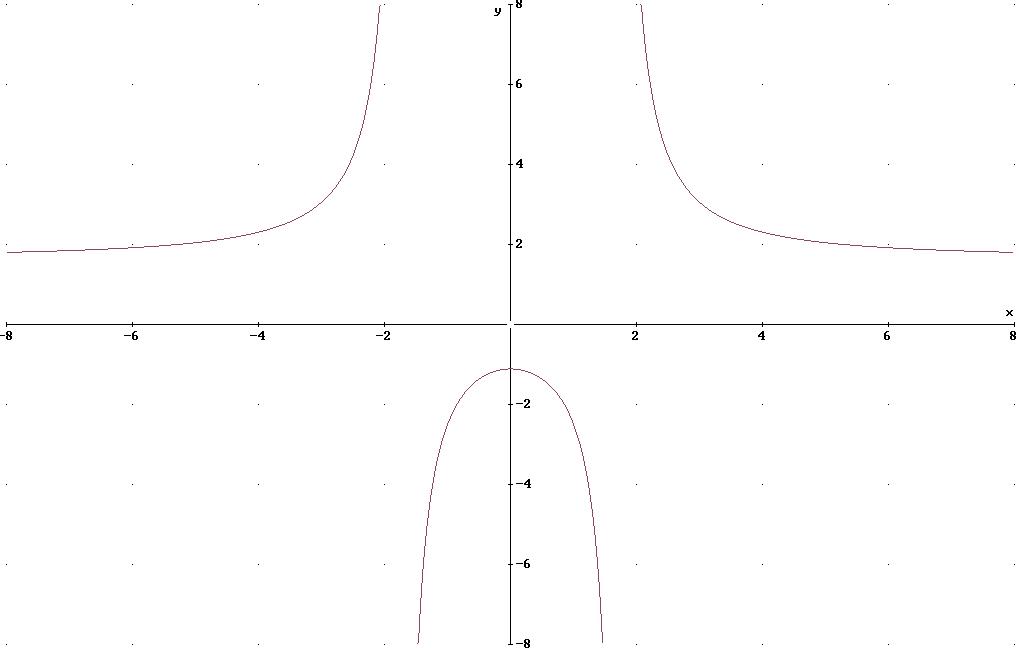Graphik: