Kurvendiskussion mit einem Parameter

Gegeben ist die Funktionsschar f_t durch die Gleichung:

Die Schaubilder seien K_t.

a) Untersuchen Sie K_t auf Symmetrie, Schnittpunkte mit den Koordinatenachsen, Extrem- und Wendepunkte. (auf Nachweis der Existenz eventuell vorhandener Wendepunkte kann verzichtet werden). Untersuchen Sie die Funktion f_t auf ihr Verhalten für.

Zeichnen Sie die Kurven K₁ und K₄ im Intervall [-2;3] in ein gemeinsames Koordinatensystem.(Wählen Sie die Einheit 2 cm)(siehe Aufgabe c)

Ableitungen:

Symmetrie:

keine Symmetrie

Schnittpunkt mit der x-Achse:

aber: Definitionsbereich t>0 !!!

Es sind keine Nullstellen vorhanden.

Schnittpunkt mit der y-Achse:

Extrempunkte:

aber: Definitionsbereich t>0 !!!

Es sind keine Extremstellen vorhanden.

Wendepunkte:

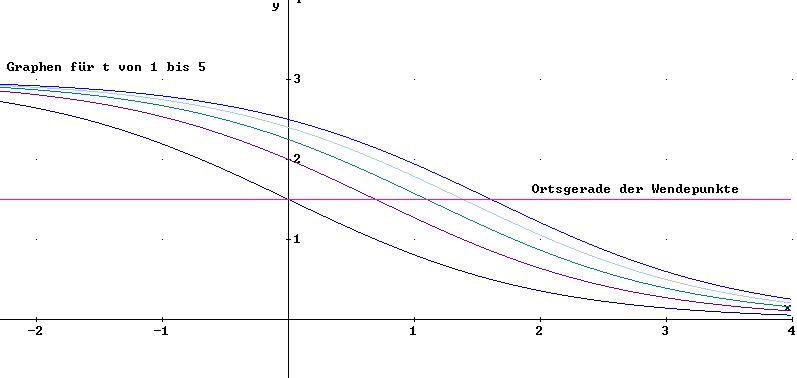
b) Geben Sie die Gleichung für die Ortskurve der Wendepunkte der Kurve K_t an.

Die Orts-”kurve” der

Wendepunkte ist eine

horizontale Linie

bei y= 1.5

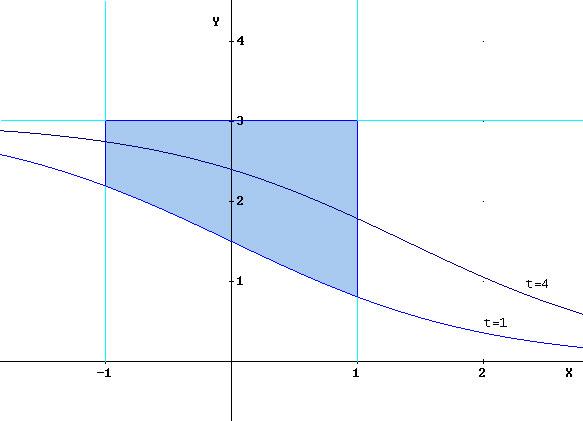
c) Die Kurve K₁ schließt mit den Geraden x= -1, x=1 und y=3 eine Fläche vollständig ein. Bestimmen Sie die Maßzahl des Flächeninhaltes.

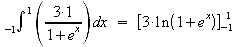
Man integriert:

Die 3 bleibt als konstanter Faktor erhalten.

=

=

=

== 3 FE

Nun hat man aber erst das Flächenstück UNTER der Kurve berechnet, dieses subtrahiert man jetzt von der Gesamtfläche des Rechtecks:

Gesamtfläche: g=2 LE (x von -1 bis 1) , h=3 LE (y von 0 bis 3)

Das gesuchte Flächenstück hat eine Fläche von 3 FE und entspricht dem Flächenstück unter der Kurve, da die diese das Rechteck im Verhältnis 1:1 teilt.