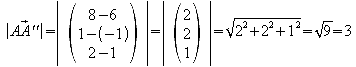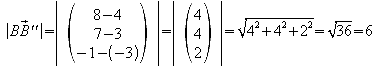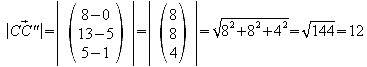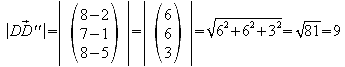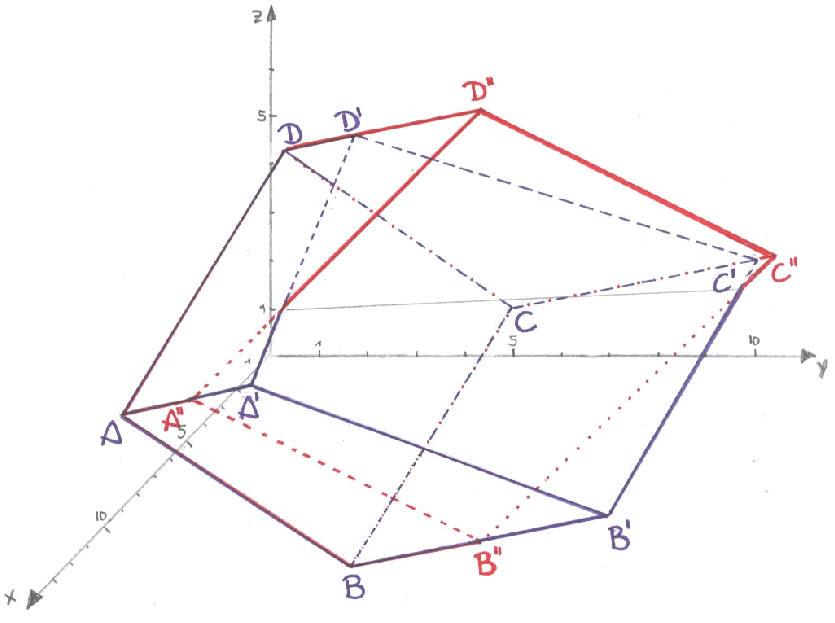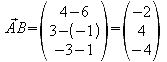
POLYEDER

1. Gegeben sind die Punkte A[6/-1/1], B[4/3/-3] und C[0/5/1].

1.1 Weisen Sie nach, dass das Dreieck ABC rechtwinklig und gleichschenklig ist

Zuerst ermittelt man alle drei Seitenlängen, um die gleichschenkligen Seiten zu ermitteln zwischen sich der rechte Winkel befinden muss. Dieser ist mit dem Skalarprodukt nachzuweisen.

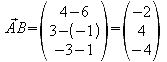
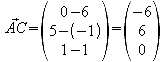
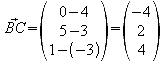
1.2 Ermitteln Sie einen Punkt D derart, dass ABCD ein Quadrat ist.

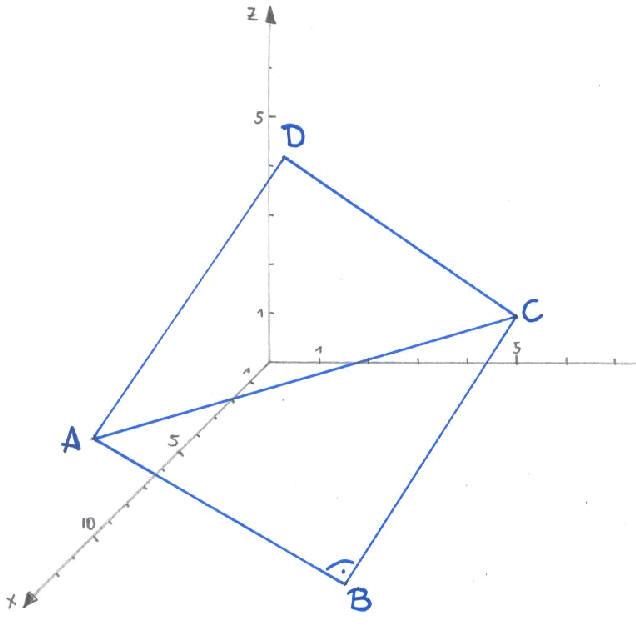
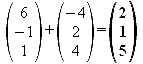
1.3 Stellen Sie eine Gleichung

der Ebene E₁ auf, in der

das Quadrat liegt.

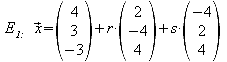
1.4 Zeigen Sie, dass die Seite AB mit der x-Achse einen Schnittpunkt hat.

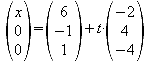
t einsetzen, x errechnen.

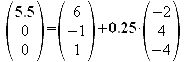Die x-Achse wird bei 5.5 geschnitten.

1.5 Wir betrachten jetzt einen Polyeder H₁: ABCDA'B'C'D' mit A'[10/3/3],

Ermitteln Sie die Koordinaten der Punkte B', C'und D', die bezüglich E₁ im gleichen Halbraum wie A' liegen.

Wir können zunächsterrechnen, da alle strecken parallel sind, kann man diesen Vektor als Richtungsvektor benutzen.

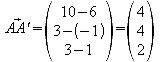
Nun addieren wir zum Ausgangspunkt (B,C oder D) den Richtungsvektor multipliziert mit dem Quotienten der Beträge (Betrag der gesuchten Strecke dividiert durch den Betrag des Richtungsvektors).

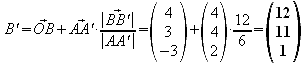
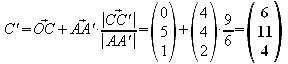
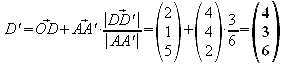
1.6 Weisen sie nach, dass die Punkte A', B', C', D' in einer Ebene E₂ liegen.

Man stellt zuerst eine Ebenengleichung mit drei Punkten (z.B. A',B',C') auf und errechnet dann mittels Hessescher Normalform, ob der vierte Punkt (D') auch auf der Ebene liegt.

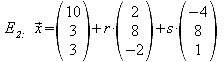
Normalenvektor: Kreuzprodukt der beiden Richtungsvektoren

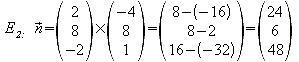
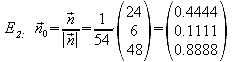
Hessesche Normalform:

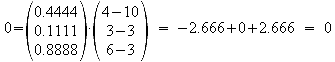
D' erfüllt die Bedingung der Hesseschen Normalform und liegt somit ebenfalls in der Ebene E₂.

1.7 Zeigen Sie, dass die Kanten AA' , BB' , CC' , DD' auf E₁ senkrecht stehen und berechnen Sie das Volumen des Polyeders H₁.

Man ermittelt den Normalenvektor von E₁, dieser muss mit dem Richtungsvektorübereinstimmen. Da alle Kanten parallel sind, reicht dieser eine Nachweis.

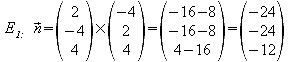
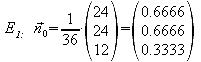
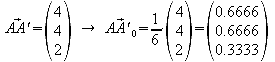
Normalenvektor der Ebene E₁ und der Richtungsvektorstimmen überein. Die Kanten AA' , BB' , CC' , DD' stehen senkrecht auf E_1.

VOLUMENBERECHNUNG:

Die Grundfläche lässt sich sehr einfach ermitteln:

Für die Höhe errechnen wir den Mittelwert der Seitenlängen:

Gesamtfläche:

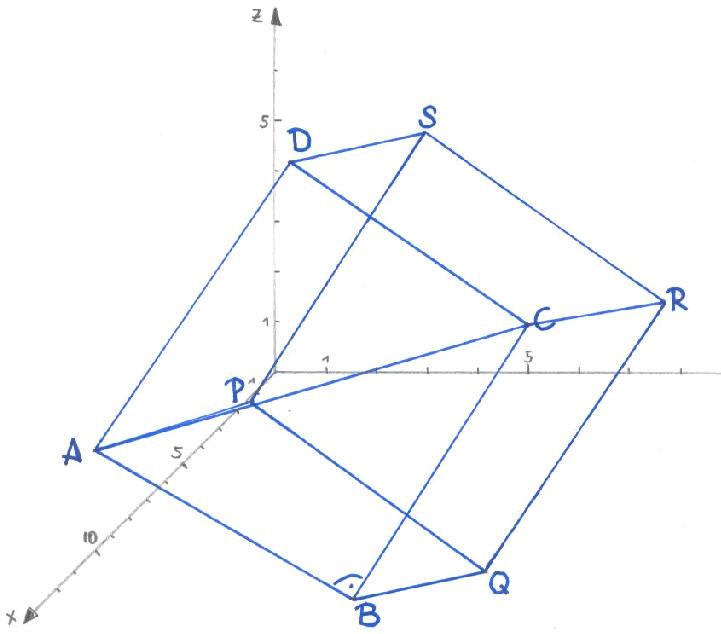
1.8 Ermitteln Sie alle Punkte P,Q,R,S, die mit A,B,C,D Eckpunkte eines Würfels sind.

Da bei einem Würfel alle Seiten gleich lang sind, müssen die Punkte P,Q,R,S also jeweils 6 Längeneinheiten von A,B,C,D entfernt sein. Der bereits errechnete Richtungsvektorhat genau diesen Betrag, was die Rechnung sehr vereinfacht.

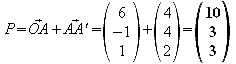
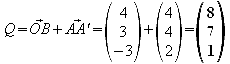
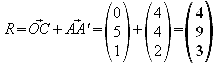
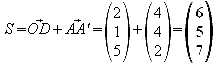
1.9 Die Längen der Kanten AA' , BB' , CC' , DD' des Polyeders H₁ werden jetzt so verändert, dass ihre Endpunkte in der Ebene E₃ mit der Gleichung x=8 liegen.

Weisen Sie nach, dass das so entstandene Polyeder H₂ zum Polyeder H₁ kongruent ist.

Man stellt die Geradengleichungen für alle vier Kanten auf. Da x=8 ermittelt man für die “x-Zeile” das t. Setzt man dieses ein, so erhält man auch die y- und z-Koordinaten.

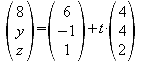
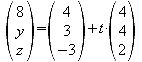
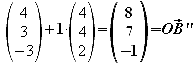
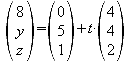
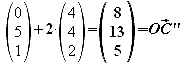
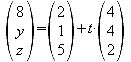
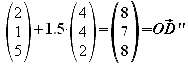
Um die Kongruenz der beiden Polyeder H₁ und H₂ nachzuweisen, errechnet man zunächst die Seitenlängen von H₂.