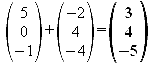
PYRAMIDEN

1. Aufgabe:

Gegeben sind die Punkte A[1/2/3], B[5/0/-1] und D[-1/6/-1]

a) Zeigen Sie, dass es einen Punkt C gibt, so dass das Viereck ABCD ein Quadrat ist. Ermitteln Sie die Koordinaten von C.

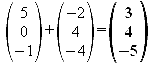
Die Seiten müssen gleich lang sein.

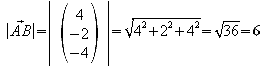
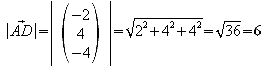
b) Das Quadrat ABCD sei die Grundfläche einer geraden Pyramide mit der Höhe h = 6 LE. Geben Sie die Koordinaten der beiden möglichen Spitzen S₁ und S₂ einer solchen Pyramide an.

Zuerst errechnet man den Einheitsnormalenvektor der Grundfläche:

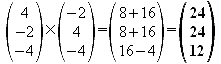
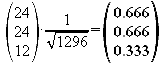
Dann errechnet man den Mittelpunkt P des Quadrates:

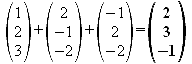
Von diesem Punkt aus, bewegt man sich nun mit dem sechsfachen Einheitsnormalenvektor nach oben bzw. unten.

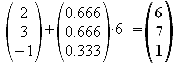
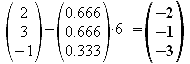
Berechnen Sie das Volumen und die Oberfläche der beiden Pyramiden.

Volumenberechnung:

Pyramidenoberfläche:

h_s = Seitenflächenhöhe

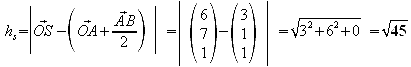
Der Oktaeder hat eine Gesamtoberfläche von 161 Flächeneinheiten.

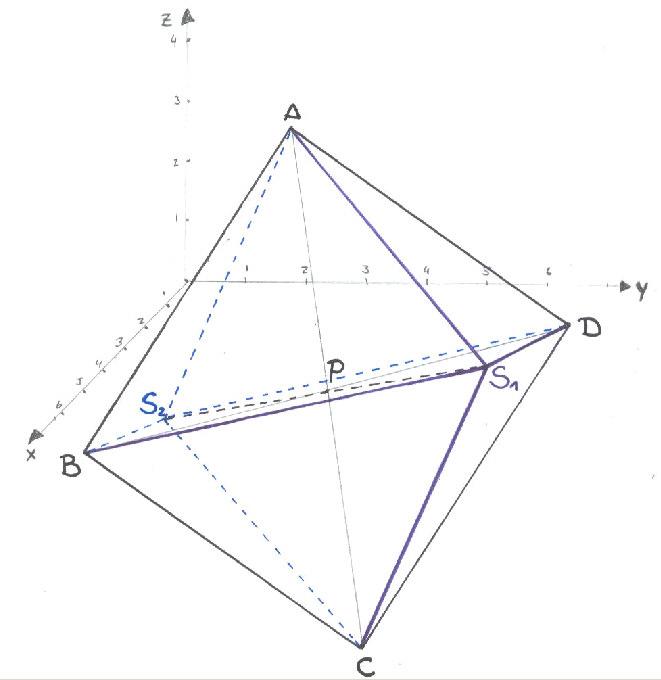Zeichnen Sie die beiden Pyramiden in ein rechtwinkliges Koordinaten- system.

c) Gegeben ist eine Gerade g durch die Gleichung: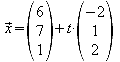

Zeigen Sie, dass das Volumen der Pyramide ABCDS₁ konstant bleibt, wenn die Spitze S₁ auf der Geraden g „wandert“.

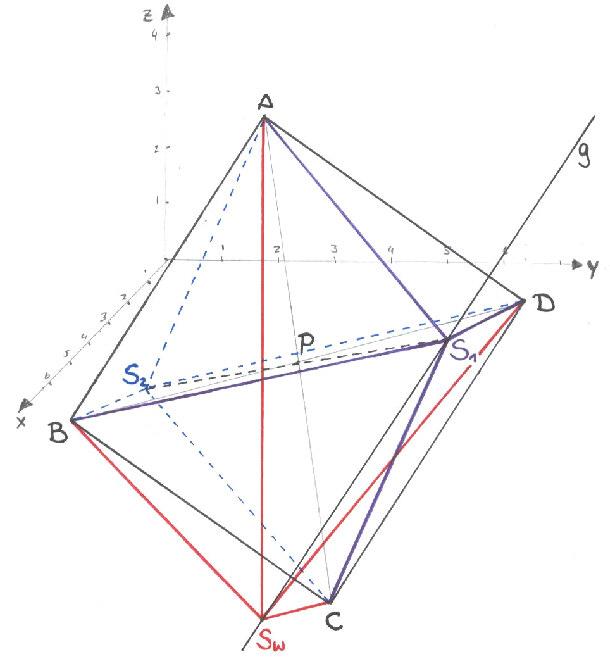Wenn der Normalenvektor der Grundfläche orthogonal zum Richtungsvektor der Gerade g ist, dann bleibt die Höhe (während S₁ auf g „wandert“) konstant und somit auch das Pyramidenvolumen.

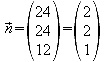
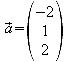
Ist das Skalarprodukt dieser Vektoren Null,

so ist die Rechtwinkligkeit nachgewiesen.

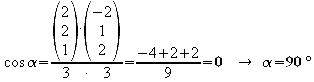
2.Aufgabe:

In einem rechtwinkligen Koordinatensystem sind die Punkte A[1/2/1], B[3/1/3], C[5/3/2], D[3/4/0] und S[1.5/5.5/4.5] gegeben.

a) Die Punkte A,B,C liegen in einer Ebene E₁.

Stellen Sie für E₁ eine Parametergleichung und eine Normalengleichung auf.

Weisen Sie nach, dass die Punkte A,B,C und D Eckpunkte eine Quadrates sind.

Parametergleichung:

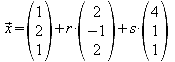
Normalenform:

Normalenvektor:

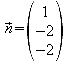
Sind die gegenüberliegenden Winkel rechtwinklig und die Seiten gleich

lang, handelt es sich eindeutig um ein Quadrat.

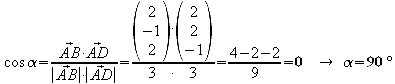
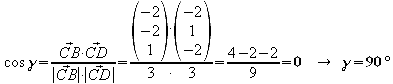
b) Der Punkt S ist die Spitze einer Pyramide ABCDS.

Berechnen Sie die Koordinaten für den Fußpunkt F des Lotes von S auf die Ebene E₁.

Mit Hilfe des Normalenvektors von E₁ und dem Punkt S erstellt man eine Geradengleichung für h. Nun lässt man die Ebene E₁ und die Gerade h schneiden, der ermittelte Spurpunkt ist der gesuchte Fußpunkt F.

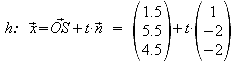
Gleichsetzen von Ebene E₁ und Gerade h:

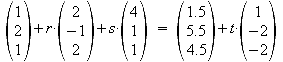
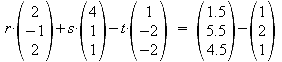
a

b 2b + c = c'

c

a

b a + 2b = b'

c'

a

b' b'– 2c'= c''

c'

a

b'

c''

Parameter ausrechnen:

Probe:

Die Koordinaten des Fußpunkt F lauten F [3/2.5/1.5].

Zeigen Sie, dass die Pyramide ABCDS gerade ist.

Der Beweis, dass die Pyramide gerade ist, kann erbracht werden, indem man nachweist, dass F der Mittelpunkt des Quadrates ABCD ist.

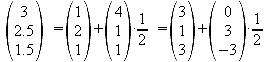
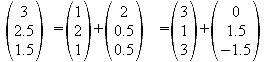
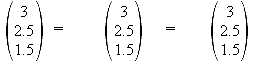
Die Pyramide ist gerade, weil die Spitze S senkrecht über dem Mittelpunkt der

Grundfläche steht.

Berechnen Sie das Volumen der Pyramide ABCDS und die Größe des Winkels zwischen Grundfläche ABCD und einer Seitenfläche der Pyramide.

Volumenberechnung:

Winkel zwischen Grundfläche und Seitenfläche:

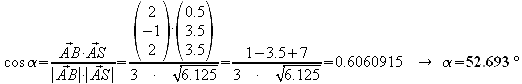
c) Die Pyramide ABCDS wird durch die Ebene E₂ mit der Gleichung -x + 2y + 2z = 9.5 geschnitten. Untersuchen Sie, ob durch diesen Schnitt ein Pyramidenstumpf entsteht.

Merkmal des Pyramidenstumpfes ist die Parallelität von Grund- und Deckfläche. Also müssen die Normalenvektoren von E₁ und E₂ untersucht werden.

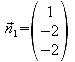und

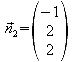
Diese Vektoren sind bis auf ihren Richtungssinn identisch. Das kann auch mit dem skalarprodukt nachgewiesen werden:

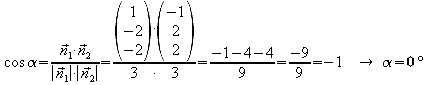
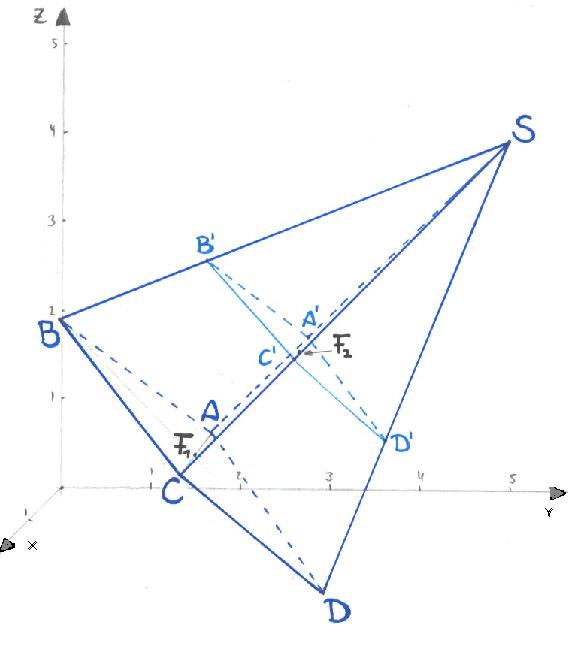
Um die Höhe des Pyramidenstumpfes

zu ermitteln, errechnet man, wo

die Ebene E₂ die Geraden h schneidet.

Über die Achsenabschnittsform erhält man drei Punkte der Ebene E₂ und kann eine dann eine Parametergleichung aufstellen.

X [9.5/0/0], Y [0/4.75/0], Z [0/0/4.75]

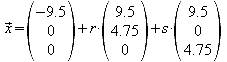
Gleichsetzen von E₂ und h:

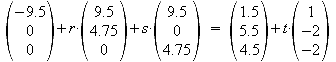
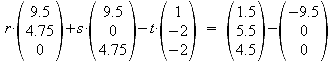
a

b 4.75 a – 9.5 b = b'

c

a

b' b' – 9.5 c = c'

c

a

b'

c'

Parameter ausrechnen:

Probe: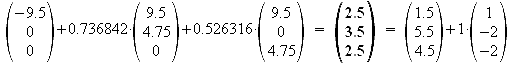

Der Mittelpunkt F₂ der Deckfläche liegt bei F₂[2.5/3.5/2.5].

Höhe des Pyramidenstumpfes:

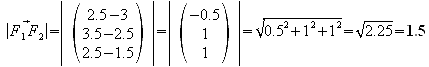
In welchem Verhältnis stehen die Volumina der Pyramide ABCDS und des Restkörpers?

Nun muss man noch mindestens zwei Punkte (A',B') ermitteln, um die obere Kantenlänge und somit auch das Volumen errechnen zu können.

Man erstellt die Geradengleichung für die Gerade, welche durch A bzw. B und die Spitze S verläuft. Diese setzt man mit der Ebene E₂ gleich und erhält den Spurpunkt A' bzw. B'.

Gerade g₁ :

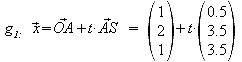
Gerade g₂ :

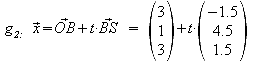
Gleichsetzen von E₂ und g₁:

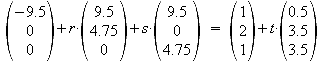
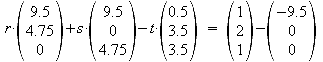
a

b 4.75 a – 9.5 b = b'

c

a

b' b' – 9.5 c = c'

c

a

b'

c'

Parameter ausrechnen:

Probe: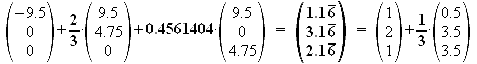

A'[1.167/3.167/2.167]

Gleichsetzen von E₂ und g₂:

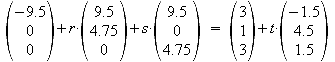
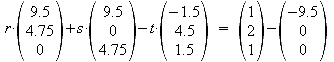
a

b 4.75 a – 9.5 b = b'

c

a

b' b' – 9.5 c = c'

c

a

b'

c'

Parameter ausrechnen:

Probe: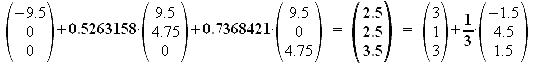

B'[2.5/2.5/3.5]

Die obere Kantenlänge entspricht der Strecke A'B':

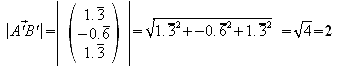
Nun hat man alle Größen ermittelt, die man zur Volumenberechnung des Pyramidenstumpfes braucht:

Verhältnis der Pyramide ABCDS zum Restkörper:

Der Pyramidenstumpf nimmt etwas mehr als zwei Drittel ( 70.37% ) der Pyramide ABCDS ein, der Restkörper ist kleiner als ein Drittel ( 29.67% ).