![]() ={0;
1; 2; 3; 4; ...}
={0;
1; 2; 3; 4; ...}
unendliche Menge
Zahlenbereich der natürlichen Zahlen
A ={1; 2; 3; 4; 5; ...}
endliche Menge
Die Menge A besteht aus den Elementen 1, 2, 3, 4 und 5.
Mengenlehre
1. Einige Grundbegriffe der Mengenlehre
1.1. Der Mengenbegriff
Definition nach Kantor :
Eine Menge ist eine Zusammenfassung bestimmter wohl unterschiedener Objekte,
unserer Anschauung oder unseres Denkens zu einem Ganzen. Die einzelnen Objekte heißen Elemente der Menge.
Mengen werden grundsätzlich durch Großbuchstaben des deutschen Alphabets ohne der Umlaute gekennzeichnet. z.B.: A, B, F, R, X, ...
Besondere Mengen haben besondere Bezeichnungen.
|
|
unendliche Menge |
Zahlenbereich der natürlichen Zahlen |
|
A ={1; 2; 3; 4; 5; ...} |
endliche Menge |
Die Menge A besteht aus den Elementen 1, 2, 3, 4 und 5. |
|
|
x ist ein Element der Menge B |
|
|
a ist kein Element der Menge B |
|
|
bedeutet leere Menge --> Zu einer leeren Menge gehört kein Element. |
Beispiel:
x2 + 4 = 0 | -4
X2 = -4
Lösung
=
![]()
Es kann beim Quadrieren keine reelle negative Zahl entstehen.
Es gibt keine Lösung.
Darstellen von Mengen
1. Aufschreiben aller Elemente einer Menge (endliche Mengen)
Menge aller Primzahlen < 10
M = {2; 3; 5; 7}
2. Mengenoperator
M =
{x|x = 2n mit
![]() }
}
Menge aller x mit der Eigenschaft “Element der natürlichen Zahlen”
x = 20 = 1; x = 21 = 2; x = 22 = 4; x = 23 = 8
M = {1; 2; 4; 8; 16; 32; ...}
3. Venn - Diagramm
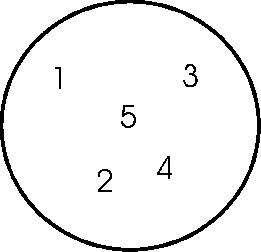
A = {1; 2; 3; 4; 5}
Elemente der Menge treten nie doppelt auf. Die Reihenfolge der Elemente spielt keine Rolle.